# !pip install yahooquery pandas_datareader arch
# !pip install keras-tunerThis model predicts stock prices (\text{UnderlyingClose}) using an LSTM neural network with volatility-informed features and Black-Scholes option Greeks. Key variables include:
- Input features: Historical close price, log returns (r_t = \ln(P_t/P_{t-1}), 20/50-day SMAs, realized volatility (\sigma_{\text{real}} = \text{20-day rolling std}(r_t) \times \sqrt{252}), GARCH(1,1) volatility (\sigma_{\text{GARCH}} estimated via maximum likelihood), risk-free rate (10-year Treasury yield), and Black-Scholes Greeks (Delta, Gamma, Theta) computed using \sigma_{\text{GARCH}}.
- Options data (retrieved but not directly used in features): Provides expiration dates and strike prices, though the current implementation uses a fixed \text{TimetoMaturity} = 30/365 for Greeks calculation, leaving options data as auxiliary information for potential future use (e.g., implied volatility integration).
Volatility computation combines short-term empirical estimates (realized) and dynamic GARCH modeling, which captures volatility clustering via σ_t^2 = ω + αr_{t-1}^2 + βσ_{t-1}^2.
LSTM suitability: The model leverages LSTM’s ability to learn temporal dependencies in the engineered feature sequences. Financial time series exhibit non-linear patterns and memory effects (e.g., volatility persistence), which LSTMs handle via gated memory cells and backpropagation through time.
Pipeline:
1. Data engineering: Fetch stock/options data, compute features/volatility/Greeks.
2. Sequencing: Convert features into 3D tensors (samples x 10-day lookback x features) for LSTM input.
3. Scaling: Normalize features/targets to [0,1] using MinMaxScaler.
4. Hyperparameter tuning: Optimize LSTM architecture (layer depth, units, dropout rates) and learning rate via Keras Tuner.
5. Training: Fit on 80% of data with early stopping, validate on 20% of training set.
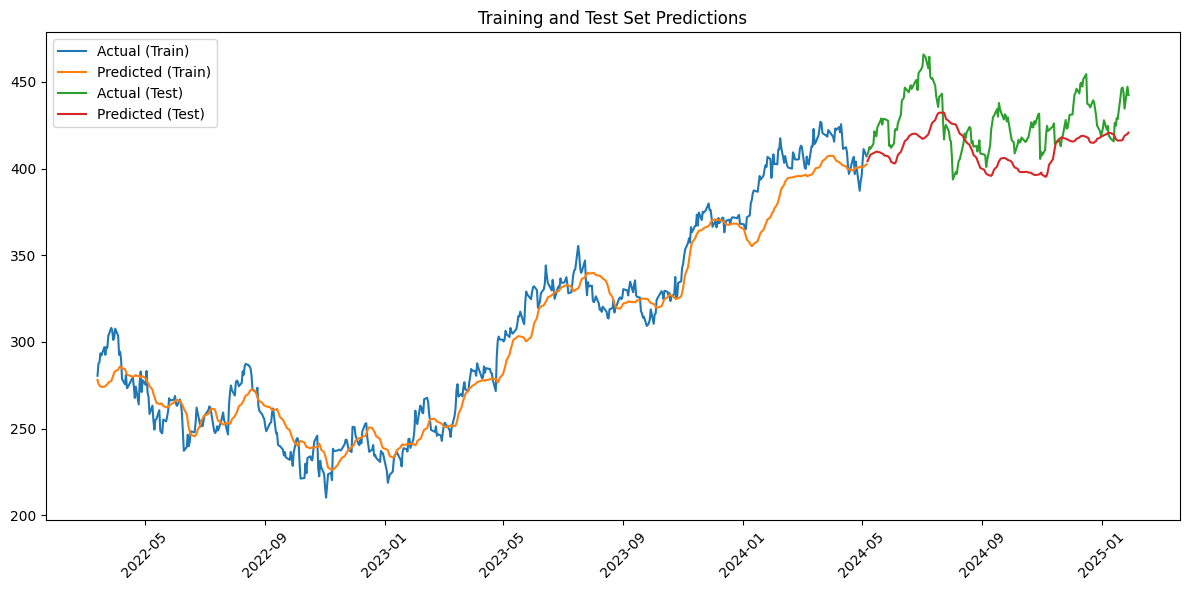
6. Evaluation: Predict next-day prices, inverse-scale outputs, and visualize date-aligned predictions vs actuals.
The integration of volatility metrics and option Greeks enhances the model’s ability to capture market uncertainty and hedging dynamics, while the LSTM architecture models complex temporal interactions between these variables.
import datetime as dt
import pandas as pd
import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt
from pandas_datareader import data as pdr
from scipy.stats import norm
from arch import arch_model
import warnings
warnings.filterwarnings("ignore", category=FutureWarning)
# --- Data and Feature Engineering ---
def build_black_scholes_dataset(ticker_symbol, start_date, end_date, option_type='call', default_T=30/365):
tk = yf.Ticker(ticker_symbol)
data = tk.history(start=start_date, end=end_date)
data = data.reset_index().set_index('Date')
data.index = data.index.tz_localize(None) # Ensure tz-naive index
data['Log_Returns'] = np.log(data['Close'] / data['Close'].shift(1))
data['Realized_Volatility'] = data['Log_Returns'].rolling(20).std() * np.sqrt(252)
data['SMA_20'] = data['Close'].rolling(20).mean()
data['SMA_50'] = data['Close'].rolling(50).mean()
returns = data['Log_Returns'].dropna() * 100
am = arch_model(returns, vol='Garch', p=1, q=1, dist='normal')
res = am.fit(disp='off')
data['GARCH_Volatility'] = res.conditional_volatility.reindex(data.index) / 100 * np.sqrt(252)
treasury = pdr.get_data_fred('DGS10', start_date, end_date) / 100
treasury.index = treasury.index.tz_localize(None)
treasury = treasury.reindex(data.index, method='ffill')
expirations = tk.options
options = []
for expiry in expirations:
try:
chain = tk.option_chain(expiry)
opt_df = chain.calls if option_type.lower()=='call' else chain.puts
opt_df['expiration'] = pd.to_datetime(expiry)
options.append(opt_df)
except:
continue
df_options = pd.concat(options) if options else pd.DataFrame()
features = pd.DataFrame({
'Underlying_Close': data['Close'],
'Log_Returns': data['Log_Returns'],
'SMA_20': data['SMA_20'],
'SMA_50': data['SMA_50'],
'Realized_Volatility': data['Realized_Volatility'],
'GARCH_Volatility': data['GARCH_Volatility'],
'Risk_Free_Rate': treasury['DGS10'],
'Time_to_Maturity': default_T
}, index=data.index)
def bs_greeks(row):
S = row['Underlying_Close']
K = S # ATM approximation
T = row['Time_to_Maturity']
r = row['Risk_Free_Rate']
sigma = row['GARCH_Volatility']
if T <= 0 or sigma <= 0:
return pd.Series([np.nan, np.nan, np.nan], index=['Delta', 'Gamma', 'Theta'])
d1 = (np.log(S/K) + (r + 0.5 * sigma**2) * T) / (sigma * np.sqrt(T))
d2 = d1 - sigma * np.sqrt(T)
if option_type.lower() == 'call':
delta = norm.cdf(d1)
theta = (-(S * sigma * norm.pdf(d1))/(2 * np.sqrt(T)) - r * K * np.exp(-r * T) * norm.cdf(d2)) / 365
else:
delta = norm.cdf(d1) - 1
theta = (-(S * sigma * norm.pdf(d1))/(2 * np.sqrt(T)) + r * K * np.exp(-r * T) * norm.cdf(-d2)) / 365
gamma = norm.pdf(d1) / (S * sigma * np.sqrt(T))
return pd.Series([delta, gamma, theta], index=['Delta', 'Gamma', 'Theta'])
greeks = features.apply(bs_greeks, axis=1)
features = pd.concat([features, greeks], axis=1)
return features, df_options
# --- Data Preparation for LSTM with Dates ---
def create_sequences(X, y, dates, lookback=10):
X_seq, y_seq, date_seq = [], [], []
for i in range(len(X) - lookback):
X_seq.append(X[i:i+lookback])
y_seq.append(y[i+lookback])
date_seq.append(dates[i+lookback])
return np.array(X_seq), np.array(y_seq), np.array(date_seq)
def prepare_data_lstm(data, target='Underlying_Close', test_ratio=0.2, lookback=10):
data = data.dropna().copy()
dates = data.index # Preserve the date index
data = data.select_dtypes(include=[np.number])
data['Target'] = data[target].shift(-1)
data = data.dropna()
dates = data.index # Updated dates after dropping NA
X = data.drop(columns=[target, 'Target']).values
y = data['Target'].values
from sklearn.preprocessing import MinMaxScaler
scaler_X = MinMaxScaler()
scaler_y = MinMaxScaler()
X_scaled = scaler_X.fit_transform(X)
y_scaled = scaler_y.fit_transform(y.reshape(-1, 1))
X_seq, y_seq, date_seq = create_sequences(X_scaled, y_scaled, dates, lookback=lookback)
split = int(len(X_seq) * (1 - test_ratio))
return X_seq[:split], y_seq[:split], date_seq[:split], X_seq[split:], y_seq[split:], date_seq[split:], scaler_X, scaler_y
# --- LSTM Model Building with Keras Tuner ---
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense, Dropout
import keras_tuner as kt
from sklearn.metrics import mean_squared_error
def build_lstm_model(hp, input_shape):
model = Sequential()
model.add(LSTM(units=hp.Int('units1', min_value=32, max_value=256, step=32),
activation='tanh',
return_sequences=hp.Boolean('return_seq1', default=False),
input_shape=input_shape))
if hp.Boolean('dropout1', default=True):
model.add(Dropout(rate=hp.Float('dropout_rate1', 0.0, 0.5, step=0.1)))
if hp.Boolean('use_second_lstm', default=True):
model.add(LSTM(units=hp.Int('units2', min_value=16, max_value=128, step=16)))
if hp.Boolean('dropout2', default=True):
model.add(Dropout(rate=hp.Float('dropout_rate2', 0.0, 0.5, step=0.1)))
model.add(Dense(1))
lr = hp.Choice('lr', values=[1e-2, 1e-3, 1e-4])
optimizer = tf.keras.optimizers.Adam(learning_rate=lr, clipnorm=1.0)
model.compile(optimizer=optimizer, loss='mse')
return model
# --- Pipeline for LSTM Training and Prediction with Date-Aware Plots ---
def run_pipeline_lstm(data, test_ratio=0.2, lookback=10, max_trials=5, epochs=100):
X_train, y_train, dates_train, X_test, y_test, dates_test, scaler_X, scaler_y = prepare_data_lstm(data, target='Underlying_Close', test_ratio=test_ratio, lookback=lookback)
tuner = kt.RandomSearch(lambda hp: build_lstm_model(hp, input_shape=X_train.shape[1:]),
objective='val_loss',
max_trials=max_trials,
directory='lstm_tuner',
project_name='lstm_options_underlying')
tuner.search(X_train, y_train, epochs=epochs, validation_split=0.2,
callbacks=[tf.keras.callbacks.EarlyStopping(monitor='val_loss', patience=5)])
best_model = tuner.get_best_models(num_models=1)[0]
history = best_model.fit(X_train, y_train, epochs=epochs, validation_split=0.2,
callbacks=[tf.keras.callbacks.EarlyStopping(monitor='val_loss', patience=5)])
# Obtain predictions for both training and test sets
y_pred_train = best_model.predict(X_train)
y_pred_test = best_model.predict(X_test)
mse_train = mean_squared_error(y_train, y_pred_train)
mse_test = mean_squared_error(y_test, y_pred_test)
print("Train MSE:", mse_train)
print("Test MSE:", mse_test)
# Inverse transform the scaled targets
y_train_inv = scaler_y.inverse_transform(y_train)
y_pred_train_inv = scaler_y.inverse_transform(y_pred_train)
y_test_inv = scaler_y.inverse_transform(y_test)
y_pred_test_inv = scaler_y.inverse_transform(y_pred_test)
# Plot training and test predictions with dates on the x-axis
plt.figure(figsize=(12,6))
plt.plot(dates_train, y_train_inv, label='Actual (Train)')
plt.plot(dates_train, y_pred_train_inv, label='Predicted (Train)')
plt.plot(dates_test, y_test_inv, label='Actual (Test)')
plt.plot(dates_test, y_pred_test_inv, label='Predicted (Test)')
plt.title("Training and Test Set Predictions")
plt.xticks(rotation=45)
plt.legend()
plt.tight_layout()
plt.show()
return best_model, scaler_X, scaler_y, tuner
if __name__ == '__main__':
features, options = build_black_scholes_dataset('MSFT', '2020-01-01', '2025-01-30')
print("Features:\n", features.tail())
print("\nOptions Data:\n", options.head() if not options.empty else "No options found")
best_model, scaler_X, scaler_y, tuner = run_pipeline_lstm(features, test_ratio=0.25, lookback=500, max_trials=10, epochs=200)Features:
Underlying_Close Log_Returns SMA_20 SMA_50 \
Date
2025-01-23 446.709991 0.001142 427.969998 429.853789
2025-01-24 444.059998 -0.005950 428.410498 430.301071
2025-01-27 434.559998 -0.021626 428.171999 430.648771
2025-01-28 447.200012 0.028672 428.626500 431.149073
2025-01-29 442.329987 -0.010950 429.216499 431.508660
Realized_Volatility GARCH_Volatility Risk_Free_Rate \
Date
2025-01-23 0.222035 0.283054 0.0465
2025-01-24 0.222987 0.270097 0.0463
2025-01-27 0.234432 0.260407 0.0453
2025-01-28 0.256044 0.271884 0.0455
2025-01-29 0.250806 0.291735 0.0455
Time_to_Maturity Delta Gamma Theta
Date
2025-01-23 0.082192 0.534931 0.010963 -0.268597
2025-01-24 0.082192 0.535007 0.011557 -0.256041
2025-01-27 0.082192 0.534744 0.012250 -0.242029
2025-01-28 0.082192 0.534645 0.011402 -0.258865
2025-01-29 0.082192 0.534478 0.010743 -0.272596
Options Data:
contractSymbol lastTradeDate strike lastPrice bid \
0 MSFT250228C00240000 2025-02-12 15:08:15+00:00 240.0 167.72 163.25
1 MSFT250228C00250000 2025-02-21 20:17:26+00:00 250.0 159.59 153.25
2 MSFT250228C00260000 2025-02-19 16:17:02+00:00 260.0 151.12 143.35
3 MSFT250228C00270000 2025-02-06 16:30:58+00:00 270.0 147.30 133.35
4 MSFT250228C00300000 2025-01-31 19:55:07+00:00 300.0 117.17 103.35
ask change percentChange volume openInterest impliedVolatility \
0 165.25 0.0 0.0 NaN 0 2.154301
1 155.25 0.0 0.0 3.0 3 2.001958
2 145.25 0.0 0.0 NaN 0 1.900391
3 135.25 0.0 0.0 1.0 0 1.753907
4 105.25 0.0 0.0 7.0 7 1.341800
inTheMoney contractSize currency expiration
0 True REGULAR USD 2025-02-28
1 True REGULAR USD 2025-02-28
2 True REGULAR USD 2025-02-28
3 True REGULAR USD 2025-02-28
4 True REGULAR USD 2025-02-28
Reloading Tuner from lstm_tuner/lstm_options_underlying/tuner0.json
Epoch 1/20014/14 ━━━━━━━━━━━━━━━━━━━━ 12s 610ms/step - loss: 0.0068 - val_loss: 0.0024 Epoch 2/200 14/14 ━━━━━━━━━━━━━━━━━━━━ 9s 535ms/step - loss: 0.0049 - val_loss: 0.0015 Epoch 3/200 14/14 ━━━━━━━━━━━━━━━━━━━━ 10s 482ms/step - loss: 0.0046 - val_loss: 0.0022 Epoch 4/200 14/14 ━━━━━━━━━━━━━━━━━━━━ 10s 482ms/step - loss: 0.0044 - val_loss: 0.0032 Epoch 5/200 14/14 ━━━━━━━━━━━━━━━━━━━━ 11s 494ms/step - loss: 0.0040 - val_loss: 0.0012 Epoch 6/200 14/14 ━━━━━━━━━━━━━━━━━━━━ 11s 580ms/step - loss: 0.0042 - val_loss: 0.0031 Epoch 7/200 14/14 ━━━━━━━━━━━━━━━━━━━━ 10s 566ms/step - loss: 0.0037 - val_loss: 0.0017 Epoch 8/200 14/14 ━━━━━━━━━━━━━━━━━━━━ 7s 486ms/step - loss: 0.0031 - val_loss: 0.0029 Epoch 9/200 14/14 ━━━━━━━━━━━━━━━━━━━━ 10s 480ms/step - loss: 0.0030 - val_loss: 0.0026 Epoch 10/200 14/14 ━━━━━━━━━━━━━━━━━━━━ 8s 575ms/step - loss: 0.0025 - val_loss: 0.0026 17/17 ━━━━━━━━━━━━━━━━━━━━ 3s 145ms/step 6/6 ━━━━━━━━━━━━━━━━━━━━ 1s 127ms/step Train MSE: 0.0014202666439744902 Test MSE: 0.003809773039157242